リーマン主要公式の第2項について

$J(x)$ と第2項について

文献[1, P22]より

と定義すると $J(x)$ は素数のべき乗 $p^n$ が現れるたびに $1/n$ だけ増加する関数となる. ただし $x$ がちょうど素数のべき乗になるときは $1/2n$ だけ増加する.

$J(x)$ はリーマンゼータ関数の零点を用いて表わせる[1, P48].

$J(x)$ の第2項は, 零点のペア $\rho,\overline\rho$ を足していくことによって収束が保証される. より厳密に書こうとすれば

となる. ここで, クリティカルライン上の零点を虚部の小さい順に並べてみよう.

クリティカルライン上には無限に零点が存在するから, 第2項を厳密に計算することはできない. 有限個の項で計算するために, 関数 $f(x)$ を以下で定義する.

次に関数 $f(x)$ の実装について述べる.

プログラム

• プログラムをPythonで作成する
• $x$ を $10$ から $50$ までとり, $f(x)$ をプロットする
• リーマンゼータ関数の零点は Odlyzko による数値計算の結果¹を用いる
• 対数積分 $\text{Li}(x)$ の計算には指数積分との関係式を利用し, scipy の expi を活用する
• $x$ が素数または素数のべき乗のときの $f(x)$ の値を調べる

# -*- encoding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import expi

# 計算に使用する零点の個数
nzeros = 500

# 零点の読み込み
# 零点のデータをダウンロードして適宜ファイルパスを修正してください
with open('/path/to/zeros.txt','r') as f:
    lines = f.readlines()
    zeros = [float(line.strip()) for line in lines[:nzeros]]

# 対数積分
def li(z):
    return expi(np.log(z))

# J(x) の第2項を有限個の項で打ち切ったもの
def f(x):
    s = 0.0
    for t in zeros:
        rho = 0.5+1j*t
        s += (li(x**rho) + li(x**(1-rho))).real
    return -s

# ラベル・目盛りの設定
plt.tick_params(labelbottom=True, labelleft=False, labelright=False, labeltop=False)
plt.title(r'$f(x)=-\sum_{i=1}^{500}\{Li(x^{\rho_i})+Li(x^{1-\rho_i})\}$')
plt.xlabel("x")
plt.ylabel(r'$f(x)$')

# 関数 f(x) のプロット
x = np.linspace(10,50,800)
y = [f(x_i) for x_i in x]
plt.plot(x, y)

# 素数と素数べきのプロット
primes = [11,13,17,19,23,29,31,37,41,43,47]
prime_powers = [16,25,27,32,49]
for p in primes:
    plt.plot(p,f(p),'ro')
for p in prime_powers:
    plt.plot(p,f(p),'go')

plt.show()

プロット

作成したプログラムを Python 3.11.9 で実行し, 下記の結果を得た.

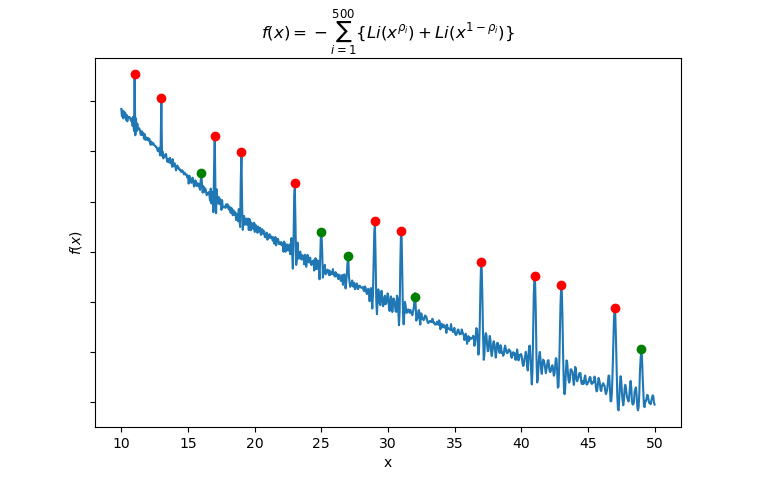
赤丸は素数 (11,13,17,19,23,29,31,37,41,43,47) , 緑丸は素数のべき乗 (16,25,27,32,49) を表す. 零点は素数の位置を"知っている"ということが, このプロットから実感できる.

追記(2025/02/02)

前回作成したプログラムが誤っていたのでプログラムを修正した.

$\text{Li}(x^\rho)=\text{Ei}(\log x^\rho)$ で計算すると np.log は $x^\rho$ の主値を計算するから, $\log x^\rho$ の虚部が $-\pi$ から $\pi$ の値しかとらなくなってしまう. 前回作成したプロットに違和感があったのはこれが原因と思われる.

対策として scipy の expi には引数として $\rho\log x$ の計算結果を渡すようにする. つまり $\text{Li}(x^\rho)=\text{Ei}(\rho\log x)$ として計算する.

そのほか, プロットを見やすくするための修正をいくつか加えた. プログラムは下記のとおり.

# -*- encoding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import expi

# 計算に使用する零点の個数
nzeros = 500

# 零点の読み込み
# 零点のデータをダウンロードして適宜ファイルパスを修正してください
# 参考URL https://www-users.cse.umn.edu/~odlyzko/zeta_tables/index.html
with open('/path/to/zeros.txt','r') as f:
    lines = f.readlines()
    zeros = [float(line.strip()) for line in lines[:nzeros]]

# J(x) の第2項を有限個の項で打ち切ったもの
def f(x):
    s = 0.0
    for zero in zeros:
        rho = 0.5+1j*zero
        #a = (li(x**rho) + li(x**(1-rho)))
        a = (expi(rho*np.log(x)) + expi((1-rho)*np.log(x)))
        s -= a.real
    return s

# ラベル・目盛りの設定
plt.figure(figsize=(16,9),dpi=120)
plt.title(r'$\text{f}(x)=-\sum_{i=1}^{500}\{\text{Li(x}^{\rho_i})+\text{Li}(x^{1-\rho_i})\}$')
plt.xlabel("x")
plt.ylabel(r'$\text{f}(x)$')
plt.xticks([11,13,16,17,19,23,25,27,29,31,32,37,41,43,47,49])

# 関数 f(x) のプロット
x = np.linspace(10,50,800)
y = [f(x_i) for x_i in x]
plt.plot(x, y,color='black',linewidth=0.8)

# 素数と素数べきのプロット
primes = [11,13,17,19,23,29,31,37,41,43,47]
prime_powers = [16,25,27,32,49]

plt.plot(11,f(11),'o',color='black',label="Prime Numbers")
plt.plot(16,f(16),'x',color='black',label="Prime Powers")

for p in primes[1:]:
    plt.plot(p,f(p),'o',color='black')
for p in prime_powers[1:]:
    plt.plot(p,f(p),'x',color='black')        

plt.legend()
plt.show()

作成した図を以下に示す.

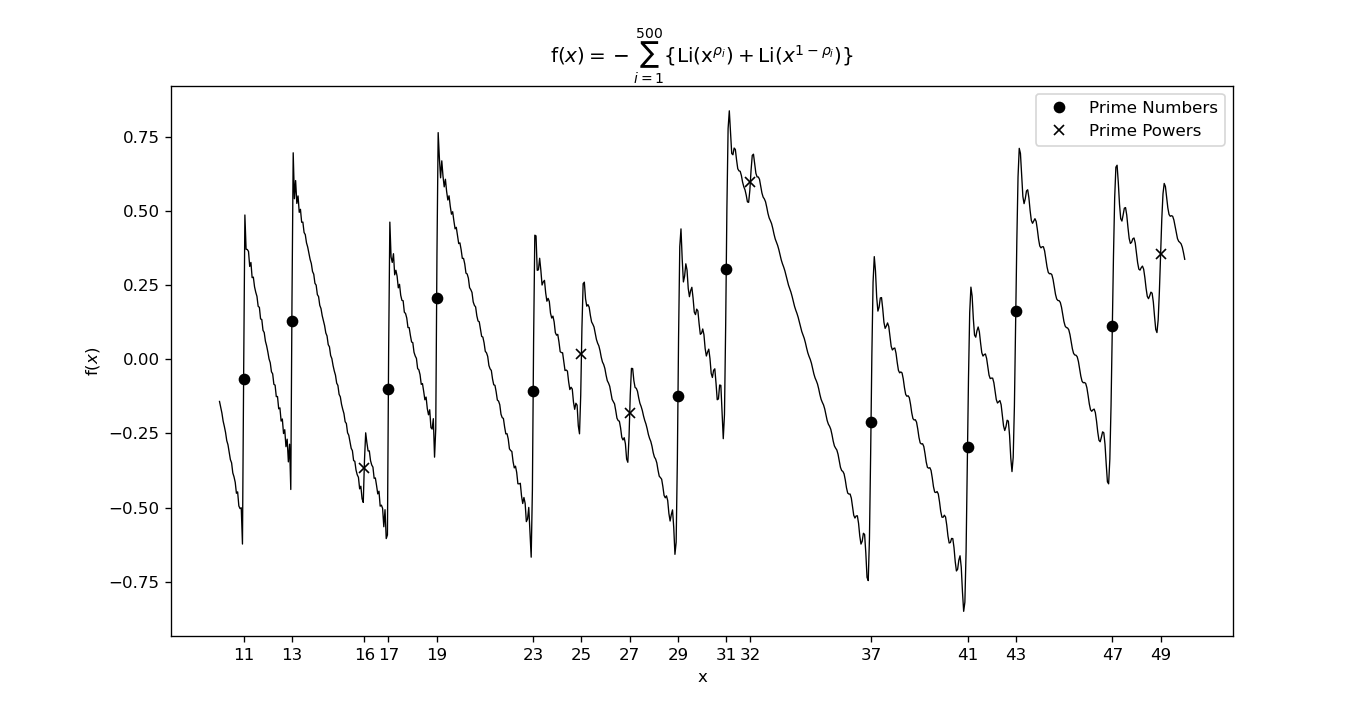
素数および素数べきで値の変化が見られる. $J(x)$ は素数べき $p^n$ に対し $1/n$ だけ増加するから, 例えば $x=16=2^4$ のときに $1/4=0.25$ だけ増加することが予想される. グラフから値を読み取ると約 $-0.50$ から約 $-0.25$ へ遷移している. つまり約 $0.25$ 増加している. 関数 $J(x)$ の4つの構成要素のうち, 第2項は段差を作り出す役割を果てしていると言えよう.

さらに追記(2025/02/02)

せっかく第2項のプロットを作成したので第1項と第2項を足した関数のプロットを作成した.

プログラムは以下のとおり.

# -*- encoding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import expi

# 計算に使用する零点の個数
nzeros = 500

# 零点の読み込み
# 零点のデータをダウンロードして適宜ファイルパスを修正してください
# 参考 https://www-users.cse.umn.edu/~odlyzko/zeta_tables/index.html
with open('/path/to/zeros.txt','r') as f:
    lines = f.readlines()
    zeros = [float(line.strip()) for line in lines[:nzeros]]

# J(x) の第2項を有限個の項で打ち切ったもの
def f(x,n):
    if n<=0:
        return 0.0
    s = 0.0
    for zero in zeros[:n]:
        rho = 0.5+1j*zero
        #a = (li(x**rho) + li(x**(1-rho)))
        a = (expi(rho*np.log(x)) + expi((1-rho)*np.log(x)))
        s -= a.real
    return s

# ラベル・目盛りの設定
plt.figure(figsize=(16,9),dpi=120)
plt.title(r'$\text{Li}(x)-\sum_{i=1}^{N}\{\text{Li(x}^{\rho_i})+\text{Li}(x^{1-\rho_i})\}$')
plt.xlabel("x")
plt.xticks([11,13,16,17,19,23,25,27,29,31,32,37,41,43,47,49])

# 第1項＋第2項 のプロット
styles = [':','--','-']
ns = [0,10,500]
labels = ["Use only the first term","N=10","N=500"]
ws = [1.3,1.3,1.0]

x = np.linspace(10,50,800)
lix = [expi(np.log(x_i)) for x_i in x]

for j in range(3):
    n = ns[j]
    y = [lix[i]+f(x[i],n) for i in range(800)]
    plt.plot(x, y,color='black',linewidth=ws[j],linestyle=styles[j],label=labels[j])
plt.legend()
plt.show()

第2項の計算に用いる項数ごとに分けてグラフを作成した. 第2項の項数を増やしていくと徐々に階段の形に近づいていくことがわかる.

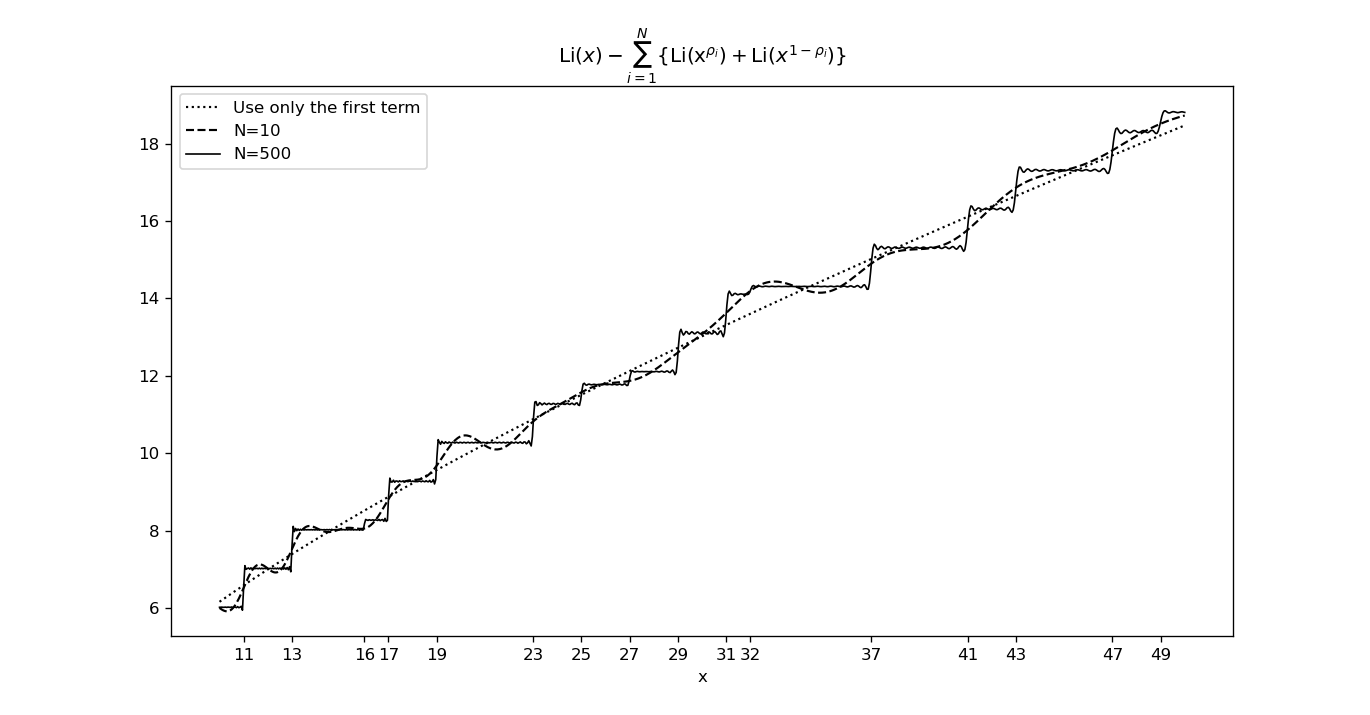
参考文献

[1] H.M.Edwards, Riemann’s Zeta Function, Dover, 2001.